现代密码学作业

学习

发布于：2023年3月4日

次浏览

Crypto

学习

字数：3.3k字

时长：13分钟

题目描述

RSA密码算法是使用最为广泛的公钥密码体制。该体制简单且易于实现，只需要选择5个参数即可（两个素数p和q、模数=N=p*q、加密指数e和解密指数d。目前来说RSA密码算法是安全，只是一些不正确的使用导致一些攻击方式。

现有人制作了一个RSA加解密软件（采用的RSA体制的参数特点描述见密码背景部分）。已知该软件发送某个明文的所有参数和加密过程的全部数据。Alice使用该软件发送了一个通关密语，且所有加密数据已经被截获，请问能否仅从加密数据恢复该通关密语及RSA体制参数？如能请给出原文和参数，如不能请给出已恢复部分并说明剩余部分不能恢复的理由？

已知所有的加密数据c以及公钥对(N, e)，对明文进行相关的破解，这是RSA攻击的基本要求。再次基础上，针对各种各样的参数选择问题，可以使用不同的攻击策略，例如指数选择的过小，或者是N重复利用、pq参数选择不当等一系列问题。

过程

RSA算法背景

RSA算法涉及三个参数N，e，d，私钥为d，公钥对为N，e。其中N=pq(p, q均为大素数)。

参数选取
1. 选取两个大素数p, q, 并计算N=pq
2. 另,选择整数e，使得,并求出e模的逆元d，即
3. 将数对公布为公钥，d保存为私钥。
加密过程：

Bob欲传递明文m给Alice，则Bob首先由公开途径找出Alice的公钥(e, N)，Bob计算加密的信息c为：
解密过程：

Bob将密文c传送给Alice。随后Alice利用自己的私钥d解密:
攻击：
1. 对N分解
  
  根据以上加解密过程，我们如果想要通过密文c获取明文m，需要获取密钥d，而获取密钥d，则必须要将N分解计算出N的欧拉函数值，而N是两个大素数p，q的积，因此将其分解是困难的。但是再特定的情况下，我们可以使用特殊方法对N进行分解，以达到破解密文的目的。
因此，我们对RSA攻击的核心步骤就是对N进行质因数分解.
1. 数学方法绕过N分解
  
  因为N的分解是困难的，并且在某些情况下，我们可以利用数论对c, e, d, n进行攻击，达到不需要d即可获取密文的效果：共模攻击、因数碰撞、低加密指数攻击等

题目背景

Alice使用的RSA密码体制，有以下事项需要说明：

模数N=pq规模为 1024 bits，其中p, q为素数；
素数p由某一随机数发生器生成；
素数q可以随机选择，也可以由（2）中的随机数发生器产生；
可以对文本加密，每次加密最多8个明文字符；
明文超过8个字符时，对明文分片，每个分片不超过8个字符；
分片明文填充为512比特消息后再进行加密，填充规则为高位添加64比特标志位，随后加上32比特通信序号，再添加若干个0，最后64比特为明文分片字符对应的ASCII码（注：填充方式参见加密案例，但注意每次通信的标志位可能变化）；
分片加密后发送一个加密帧数据，帧数据文件名称为FrameXX，其中XX表示接收序号，该序号不一定等于通信序号；
帧数据的数据格式如下，其中数据都是16进制表示，结构如下:

1024bit 模数 | 1024bit 加密指数 | 1024bit 密文
由于Alice初次使用该软件，可能会重复发送某一明文分片。

攻击方式

对于本题目除了上面讲述的针对RSA的攻击方式，还有其他的通用攻击方式。

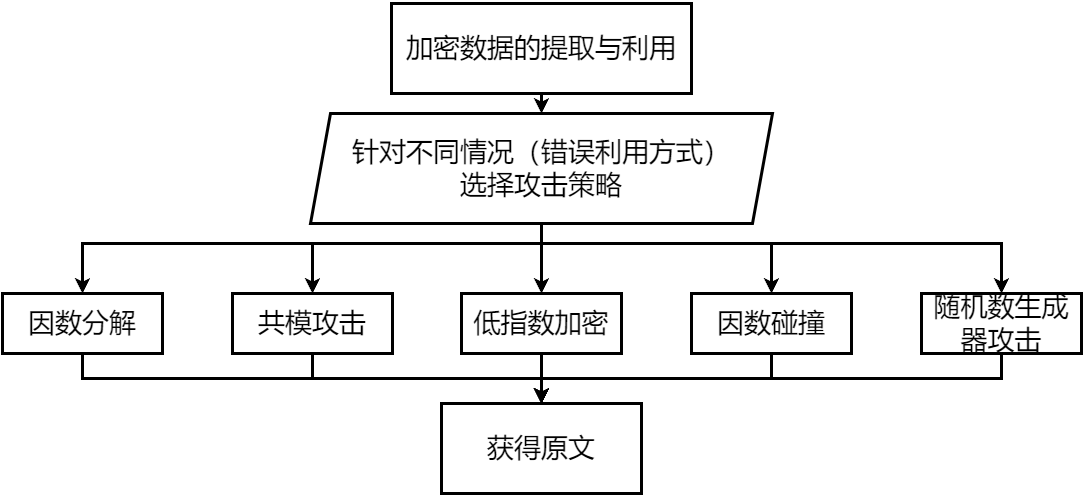
分解N

根据RSA加解密过程，我们如果想要通过密文c获取明文m，需要获取密钥d，而获取密钥d，则必须要将N分解计算出N的欧拉函数值，而N是两个大素数p，q的积，因此将其分解是困难的。但是再特定的情况下，我们可以使用特殊方法对N进行分解，以达到破解密文的目的。

直接分解n

Fermat质因数分解

当大整数N的两个因子p和q相近时，我们可以通过费马分解的办法很快分解大整数, 原理如下:

由于与相差不大, 所以相对于和来说可以忽略不计, 所以有,也就是说通过不断尝试就可以把和给计算出来了

对于帧10我们采取 Fermat因数分解这种攻击策略。

def fermat(self, N):
	a = isqrt(N)
	b2 = a * a - N
	b = isqrt(N)
	count = 0
	while b * b != b2:
		a = a + 1
		b2 = a * a - N
		b = isqrt(b2)
		count += 1
	p = a + b
	q = a - b
	assert N == p * q
	return p, q

Pollard rho p-1

若所选取的p q不为强素数，即p-1或q-1没有大素数因子时，可能存在pollard p-1分解法实现对N的因子分解。如果p q都不超过次方, 若其中一个 (p−1)或 (q−1)的因子都很小的时候（适用于p-1或q-1能够被小素数整除的情况,在这里为了方便说明我们假设为 (p−1) ,可以如下操作:

选取一个整数 k, 使其满足
由费马小定理知道,a与p互素的时候有所以, 即
那么对于N与必有公因数为, 这样就可以把N分解出来了。但是对于k的选取还是有要求的，太小了不会成立，太大了花费时间会很多。

使用这种方法可以破译Frame 2 ， Frame 6 ， Frame 19

def Pollard_p_1(self, N):
	"""
	Pollard p-1 算法
	:param N:   大整数N
	:return:    因子 P Q
	"""
	a = 2
	f = a
	while 1:
		for n in range(1, 200000):
			f = gmpy2.powmod(f, n, N)
			if is_prime(n):
				d = gcd(f - 1, N)
				if 1 < d < N:
					return d, N // d
				elif d >= N:
					f = next_prime(a)
					break
		else:
			break

在线查询

API example:
  https://api.justyy.workers.dev/api/factor/?cached&n=9223372036854775807
returns: 
{
  "result": "9223372036854775807: 7 7 73 127 337 92737 649657",
  "cached": false
}

通过公约数分解(因数碰撞)

帧1，18就使用了这种攻击方法。

如果在两次公钥的加密过程中使用的n1和n2具有相同的质因子，那么可以利用欧几里得算法直接将n1和n2分解。通过欧几里得算法可以直接求出n1和n2的最大公约数p,

那么：

而欧几里得算法的时间复杂度为：O(log n)。即便是 4096 bit 也是 1s

def Common_factor_decomposition(frames):
	frames_cnt = len(frames)
	for i in range(frames_cnt):
		for j in range(i+1, frames_cnt):
        	c1 = outer.c[i]
			c2 = outer.c[j]
			n1 = outer.n[i]
			n2 = outer.n[j]
			p = gmpy2.gcd(n1, n2)
			q1 = n1/p
			q2 = n2/p
			if gmpy2.is_prime(p) and gmpy2.is_prime(q1) and gmpy2.is_prime(q2):
	            m1 = decrypt(c, p, q)
	            m2 = decrypt(c, p, q)
                print(f"[*] {i}_th, {j}_th have same factor: {q}")

维纳攻击（低解密指数攻击）

Wiener 表示如果满足, 那么一种基于连分数的特殊攻击类型就可以危害 RSA 的安全。此时需要满足, 如果满足上述条件，通过 Wiener Attack 可以在多项式时间中分解 N，思路如下：

这个式子两边同除可得：

同样是一个很大的数，所以略大于 , e和 N 是我们是知道的，公钥中给我们的，所以我们计算出 eN后，比它略小的 kd 用计算 eN 的连分数展开，依次算出这个分数每一个渐进分数，由于 eN 略大于 kd，wiener 证明了，该攻击能精确的覆盖 kd。

本次实验没有用上该方法。

# -*- coding: cp936 -*-
import gmpy2
import time

# 展开为连分数
def continuedFra(x, y):
    cF = []
    while y:
        cF += [x / y]
        x, y = y, x % y
    return cF

def Simplify(ctnf):
    numerator = 0
    denominator = 1
    for x in ctnf[::-1]:
        numerator, denominator = denominator, x * denominator + numerator
    return (numerator, denominator)

# 连分数化简
def calculateFrac(x, y):
    cF = continuedFra(x, y)
    cF = map(Simplify, (cF[0:i] for i in xrange(1, len(cF))))
    return cF

# 解韦达定理
def solve_pq(a, b, c):
    par = gmpy2.isqrt(b * b - 4 * a * c)
    return (-b + par) / (2 * a), (-b - par) / (2 * a)

def wienerAttack(e, n):
    for (d, k) in calculateFrac(e, n):
        if k == 0: continue
        if (e * d - 1) % k != 0: continue

        phi = (e * d - 1) / k
        p, q = solve_pq(1, n - phi + 1, n)
        if p * q == n:
            return abs(int(p)), abs(int(q))

不分解N

因为N的分解是困难的，并且在某些情况下，我们可以利用数论对c, e, d, n进行攻击，达到不需要d即可获取密文的效果：共模攻击、因数碰撞、低加密指数攻击等

低加密指数攻击

帧3，8，12，16，20可使用这种方法进行攻击。

在加密过程中，如果e均较小时（加解密过程速度变快），有两个情况：

如果，那么mod一个大数N，相当于没有mod，这个时候，自然
如果，那么我们知道，但是k不够大，我们可以试出来，这个时候

def low_encryption_exponent_attack(c, n, e_max=100, k_max=100):
    for e in range(1, e_max):
        for k in range(k_max):
            c_prime = c + k*n
            rel = gmpy2.iroot(c_prime, e)
            if rel[1]:
                m = rel[0]
                return m

低加密指数广播攻击

如果选取的加密指数较低，并且使用了相同的加密指数给一个接受者的群发送相同的信息，那么可以进行广播攻击得到明文。选取了相同的加密指数 e（这里取 e=3），对相同的明文 m 进行了加密并进行了消息的传递，那么有：

对上述等式运用中国剩余定理，在 e=3 时，可以得到：

通过对进行三次开方就可以求得明文

def CRT(mi, ai):
	"""
	中国剩余定理
	:param mi:  模数
	:param ai:  余数
	:return:    M
	"""
	M = reduce(lambda x, y: x * y, mi)
	ai_ti_Mi = [a * (M // m) *  gmpy2.invert(M // m, m) for (m, a) in zip(mi, ai)]
	return reduce(lambda x, y: x + y, ai_ti_Mi) % M

def small_e_boardcast_attack(nlist, e, clist):
        m = CRT(nlist, clist)
        tmp = gmpy2.iroot(m, e)
        if tmp[1] == 1:
            return tmp[0]
        else:
            return 0

共模攻击

共模攻击即用两个及以上的公钥(N, e), 来加密同一条信息m, 设两个用户的公钥分别为且两者互质。明文消息为，密文分别为:

当攻击者截获后，就可以恢复出明文。用扩展欧几里得算法求出中的r s，由此可得:

通过上述方法就可以在不知道私钥的情况下成功还原出原本的明文。

帧0，4可以使用这种攻击方法。

def same_module_attack(N, e1, e2, n1, n2):
	print(f"[+] 共模攻击")
	d1 = gmpy2.invert(e1, e2)
	d2 = (d1 * e1 - 1) // e2
	true_c2 = gmpy2.invert(c2, N)
	m = (gmpy2.powmod(c1, d1, N) * gmpy2.powmod(true_c2, d2, N)) % N

通用攻击

这里的攻击方式，并非是针对RSA的攻击，除了RSA其他密码算法也可以通用

猜测明文攻击

我们可以根据我们获取的部分明文，对剩余明文进行猜测，猜测后，再带入到加密算法中，对密文进行比对。

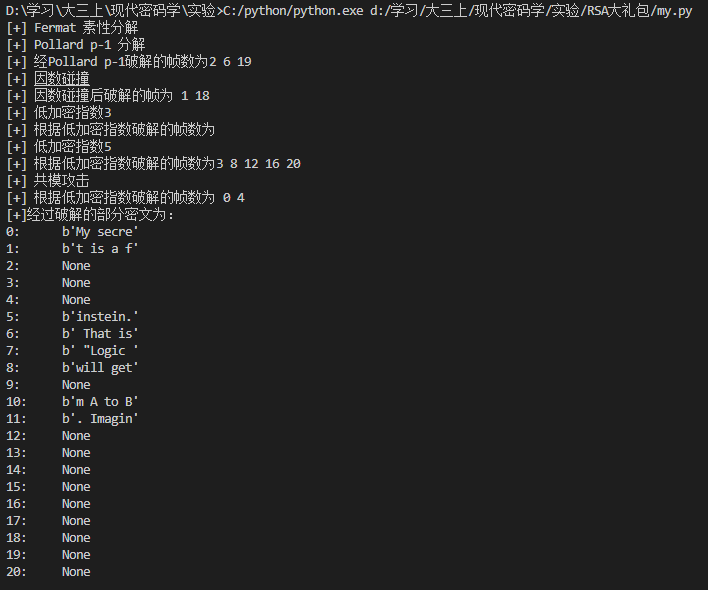
送过检索和猜测，我们得出明文是：

My secret is a famous saying of Albert Einstein. That is "Logic will get you from A to B. Imagination will take you everywhere."

我们再将该信息加密，可以还原回密文，证明我们猜测正确。

随机数生成器攻击

在本题中强调了，本题的p均是通过随机数生成器生成的，那么我们猜测本题中的随机数生成器是不安全的，假设其为线性同余（线性同余是最常见的不安全随机数生成器，例如：GCC random函数），然后通过试错法确定该随机数生成器的位数——16bit。我们尝试使用Frame1中的两个素数（p、q不定）。对与其中一个素数

72732681634652934719336436749080271209290965360454296823003471302263984423914189568624761737988340573922478722744413205121585254164070445166 75402521694747

它的二进制第一组16bits为1000101011011110第二组16bts为1111111010000101线性同余式可设为由于求解带未知模数的同余式是困难的（解不唯一），先假设,然后尝试求解同余式方程组，观察是否有满足方程组的解。解得a=365 b=1，得到递推式

我们再尝试计算多个数值发现正确。

总结

这次的密码学实验内容相对较全面，涉及的RSA问题类型都属于CTF比赛中最常见、入门难度的范畴。总的来说，这些问题的解题思路和代码实现并不十分困难，但是需要花费一定的时间和精力来理解每种方式的数学原理，以及在理解后如何通过代码正确地实现每个简单的算法。通过这次实验我学会了RSA相关的基础攻击方式，并锻炼了我自己的代码能力。